In Part 1 of this series, I explored the nature of volatility and tips on how to add volatility to your game without turning players off. In Part 2, I want to explore how to maintain the same volatility in a game even as the player count increases.

In my first article, I considered the volatility of the number of points a player can score on their turn. Now, I want to consider the volatility of the point differential of the final scores between the top player and bottom player. How likely is one player going to pull far ahead? How likely can one player come from behind to win?

THIS MEASURE OF VOLATILITY WILL LET US KNOW HOW “SWINGY” THE FINAL SCORE OF A GAME IS LIKELY TO BE WITH DIFFERENT PLAYER COUNTS.

One quick note: I use volatility and standard deviation interchangeably in this article, so if you see standard deviation, I am referencing volatility. In strict mathematical terms, volatility is derived from standard deviation, not identical to standard deviation, but for the purpose of this article, the conclusions are the same whether I am talking about volatility or standard deviation.

Let’s take another look at the popular game, Carcassonne, which can be played by 2-6 players. How does the volatility of the point differential change from 2 to 6 players in Carcassonne?

I WOULD WAGER THAT THE VOLATILITY DECREASES. HERE ARE THE REASONS WHY.

1. First, since the same number of tiles are used in every game, I would wager the total expected number of points scored by all players is probably the same if not lower as the player count increases. With more players, there are more players trying to prevent you from finishing your castle or road, and you have fewer tiles to try to finish your castle or road.
2. Second, since there is a fixed number of tiles for all player counts, the number of turns per player decreases. While it’s true the points per player per turn is the same for all player counts, there are fewer turns for players to zoom ahead or catch up.

Below is a simple model for a Carcassonne game. I just made up a value for the total points (100) and 88 is the number of tiles in the base game plus the river tiles. But the idea is that both of those values are fixed for all player counts. I chose 20% as the skill difference between the first and last player, but changing this percentage doesn’t change the overall conclusion that the standard deviation decreases with more players.

Final Score Range = [Average Point Share] +- [Turns Per Player] x [Skill Difference] x [Points Per Player Per Turn]

Total Points: 100
Total Turns: 88

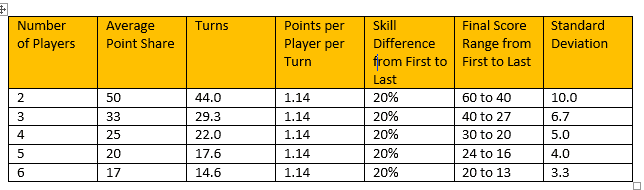
As you can see, the standard deviation of the difference between 60 and 40 is much higher than the standard deviation of the difference between 20 and 13. As the player count increases, the point differential decreases substantially.

In Dominion, the number of Victory cards does not change from 3 to 4 players, so the amount of points available does not change as the player count increases.

I would wager that the number of game turns is probably about the same regardless of the number of players. While it’s true more players could mean more attack cards, I think in general the number of turns for players to build their decks good enough to purchase Provinces is relatively independent of the player count. So, if the total points remains the same and the number of turns remains the same, the volatility of the final scores has to decrease from 3 to 4 players. I just picked 20 as the total turns, but the point is that it’s the same for both 3 and 4 players. Here’s a simple model of Dominion for 3 and 4 players:

Total Points: 96
Total Turns: 20

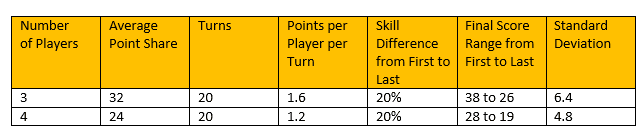
Now, if you own both Dominion and Dominion Intrigue, the easy solution is to pool your Province cards together and play with 16 Province cards in a 4 player game. It will increase the game length, but the volatility of the game will remain the same between 3 and 4 players.

One thing I should emphasize is that volatility is only one characteristic of a game. There is no one perfect volatility for all games, and higher volatility is not always better. However, many times it may be important to a game designer that the game feel the same for all player counts and volatility could definitely vary widely depending on the number of players.

SO, WHAT IS A GAME DESIGNER TO DO IF THEY WANT TO KEEP THE SAME VOLATILITY EXPERIENCE FOR ALL PLAYER COUNTS? HERE ARE TWO SOLUTIONS.

SOLUTION #1: INCREASE THE TOTAL POINTS AVAILABLE AS THE PLAYER COUNT INCREASES

This is the most straightforward way to maintain the same volatility across all player counts. Many games do this, but not all, and maybe it’s because of worries the game will take too long. That’s a valid concern.

A game like El Grande uses a novel twist on this solution by increasing the number of scoring opportunities as the player count increases. In El Grande, there are 3 main scoring phases, but 1/3 of the action cards in the game are Special Scoring cards which lets one or more players score points. With more players, more and more of these Special Scoring action cards come into play which effectively increases the total possible points as the player count increases.

As a general rule, as you increase the number of players, you should also increase the total possible points and/or the number of scoring opportunities; otherwise, the game play experience will become more flat with more players.

SOLUTION #2: UTILIZE A “POKER POT” MECHANIC

The beautiful thing about poker is that the volatility of the game stays the same even with more players; in fact, the player’s perception is that the volatility increases with more players. This is because each player adds their initial buy-in to the pool of possible winnings and the pot mechanism leads to temporary player elimination allowing one person to win a large amount on one turn. Many board games utilize the “poker pot” mechanic such as Taj Mahal and Incan Gold, but I would like to take a closer look at Incan Gold.

In Incan Gold, the treasure cards consist of the values [1, 2, 3, 4, 5, 5, 7, 7, 9, 11, 11, 13, 14, 15, 17]. In game play, a group of 2-8 players go into a cave and encounters either treasure cards or obstacles cards. Any treasure card encountered is split evenly among the players still in the cave with any leftover treasure placed on the card. If the players encounter the same obstacle twice in the cave, any players still in the cave lose all their treasure collected in the cave. So, after every revealed card, every player secretly decides to keep going in the cave or return to the safety of the camp, keeping any treasure they collected in the cave. Additionally, players who return to camp, split any treasure leftover on the revealed treasure cards.

If you have ever played Incan Gold, you know the best feeling is to be the last person in the cave since any treasure card revealed is all yours. As you can see from the chart below, the standard deviation of the treasure deck changes dramatically depending on the number of players still in the cave:

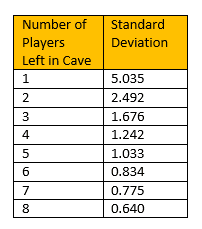
The key idea behind this table is whether you are playing 2 players, 4 players or 8 players, every player has a chance at the highest standard deviation if they are the last player left in the cave. The potential jackpot for this player can be huge especially if they know the remaining treasure cards in the deck are still the big ones.

To tie in some ideas from my first article, Incan Gold allows players to really choose the volatility of their strategy. Some players like to grab a little treasure and then go back to camp, playing it safe. Other players like to keep going in the cave even when the odds are seemingly against them.

After seeing 6 cards, the odds of getting a second matching obstacle vary a lot based on how many obstacles have been seen so far:

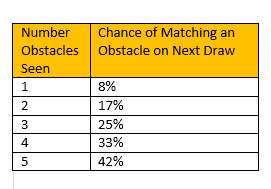
Having played the game a lot, I notice that players tend to get squeamish after seeing 3 different obstacles, but after 6 cards, the odds of getting a matching obstacle are only 1/4. Even getting 4 different obstacles after 6 cards is not so bad with odds of 1/3 of getting a match on your next draw.

To summarize the pot mechanic:

1. Allow for pots with variable awards that can increase as the player count increases
2. Allow for players to drop out of contention for the pot so that just one person can win the entire pot. Usually, the people who remain in contention the longest risk losing points.

Do you have other ideas for how to maintain your game’s volatility experience as you increase the player count? Please share in the comments. I’d love to hear your perspective.